前回の記事でDNCLの「演習問題3」~「10 二次元配列」までご説明しました。
今回も「なでしこ」というサイトの「なでしこ3簡易エディタ」を使ってプログラムを書いていきます。
必ず1行目に半角で「!DNCL2」もしくは全角で「!DNCL2」と記述してください。
引用元:なでしこ3簡易エディタ
著作権:kujirahand
演習問題4
これまで学習した知識を使って以下のプログラムを作ってみましょう。
ルール1) 以下はストイックなフリーターの1か月の労働時間が書かれた表である
| 2025年 9月 | 月 | 火 | 水 | 木 | 金 | 土 | 日 |
|---|---|---|---|---|---|---|---|
| 第1週 | 10 | 12 | 14 | 12 | 10 | 8 | 8 |
| 第2週 | 12 | 12 | 14 | 14 | 10 | 10 | 10 |
| 第3週 | 12 | 15 | 11 | 12 | 10 | 8 | 12 |
| 第4週 | 15 | 12 | 14 | 12 | 15 | 14 | 12 |
| 第5週 | 19 | 18 |
ルール2)この人は月~日まで毎日違う仕事をしており以下はそれぞれの曜日ごとの労働の時給(円)である
| 月 | 火 | 水 | 木 | 金 | 土 | 日 | |
|---|---|---|---|---|---|---|---|
| 時給 | 1200 | 1350 | 1150 | 1200 | 1300 | 1500 | 1800 |

ルール3)この人の収入の各曜日ごとの合計金額と1か月の合計金額を表示しなさい
以下はプログラムを実行したときのイメージ
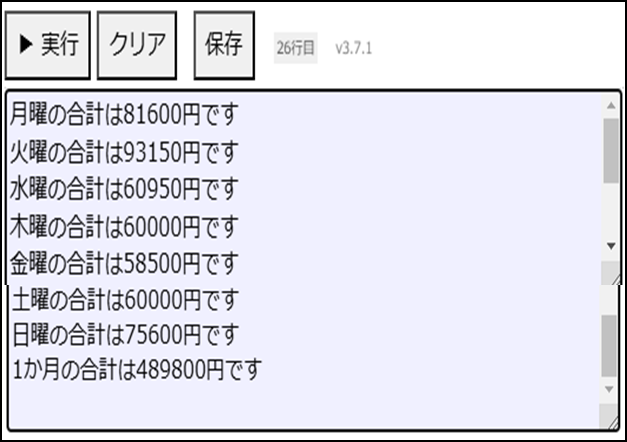
演習問題4解答1(二重ループを使わない方法)
!DNCL2
Work = [[10,12,14,12,10,8,8],[12,12,14,14,10,10,10],[12,15,11,12,10,8,12],[15,12,14,12,15,14,12],[19,18]]
Jikyu = [1200,1350,1150,1200,1300,1500,1800]
#月曜
goukeige = (Work[0][0] + Work[1][0] + Work[2][0] + Work[3][0] + Work[4][0]) * Jikyu[0]
#火曜
goukeika = (Work[0][1] + Work[1][1] + Work[2][1] + Work[3][1] + Work[4][1]) * Jikyu[1]
#水曜
goukeisu =(Work[0][2] + Work[1][2] + Work[2][2] + Work[3][2]) * Jikyu[2]
#木曜
goukeimo =(Work[0][3] + Work[1][3] + Work[2][3] + Work[3][3]) * Jikyu[3]
#金曜
goukeiki =(Work[0][4] + Work[1][4] + Work[2][4] + Work[3][4]) * Jikyu[4]
#土曜
goukeido = (Work[0][5] + Work[1][5] + Work[2][5] + Work[3][5]) * Jikyu[5]
#日曜
goukeini = (Work[0][6] + Work[1][6] + Work[2][6] + Work[3][6]) * Jikyu[6]
goukei = goukeige + goukeika + goukeisu + goukeimo + goukeiki + goukeido + goukeini
表示する("月曜の合計は" , goukeige , "円です")
表示する("火曜の合計は" , goukeika , "円です")
表示する("水曜の合計は" , goukeisu , "円です")
表示する("木曜の合計は" , goukeimo , "円です")
表示する("金曜の合計は" , goukeiki , "円です")
表示する("土曜の合計は" , goukeido , "円です")
表示する("日曜の合計は" , goukeini , "円です")
表示する("1か月の合計は" , goukei , "円です")演習問題4解答2(二重ループを使う方法)
曜日ごとの合計をループで求めるには以下のように行と列を入れ替えた形の二次元配列を考える必要があります。
| 2025年 9月 | 第1週 | 第2週 | 第3週 | 第4週 | 第5週 |
|---|---|---|---|---|---|
| 月 | 10 | 12 | 12 | 15 | 19 |
| 火 | 12 | 12 | 15 | 12 | 18 |
| 水 | 14 | 14 | 11 | 14 | |
| 木 | 12 | 14 | 12 | 12 | |
| 金 | 10 | 10 | 10 | 15 | |
| 土 | 8 | 10 | 8 | 14 | |
| 日 | 8 | 10 | 12 | 12 |
!DNCL2
Work = [[10,12,12,15,19],[12,12,15,12,18],[14,14,11,14],[12,14,12,12],[10,10,10,15],[8,10,8,14],[8,10,12,12]]
Jikyu = [1200,1350,1150,1200,1300,1500,1800]
Youbi = ["月曜" , "火曜" , "水曜" , "木曜" , "金曜" , "土曜" , "日曜"]
goukei= 0
iを0から(要素数(Work)-1)まで1ずつ増やしながら繰り返す:
goukeijikan = 0
jを0から(要素数(Work[i])-1)まで1ずつ増やしながら繰り返す:
goukeijikan = goukeijikan + Work[i][j]
youbigoukei = goukeijikan * Jikyu[i]
表示する(Youbi[i] , "の合計は" , youbigoukei , "円です")
goukei = goukei + youbigoukei
表示する("1か月の合計は" , goukei , "円です")11 組み込み関数
関数とは何かの処理を1つのかたまりとしてまとめた物のことで必要に応じて呼び出して使用します。
プログラミング言語に元から用意されている関数のことを「組み込み関数」と呼び、組み込み関数は何種類も用意されていて、それぞれ使い方と処理内容が異なります。
実際にいくつか組み込み関数の例を見てみましょう。
「最大値」という関数は、呼び出す際に「引数(ひきすう)」と呼ばれる値を( )の中に複数個カンマで区切って入れるとその引数の中で一番大きな値を戻します。
「最小値」という関数も、使い方は「最大値」と同じですが、一番小さな値を戻します。
!DNCL2
X = 最大値(10 , 50 , 100 , 20 , 60 , 120 , 5)
Y = 最小値(10 , 50 , 100 , 20 , 60 , 120 , 5)
表示する("一番大きな数字は", X , "です")
表示する("一番小さな数字は", Y , "です")上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます。
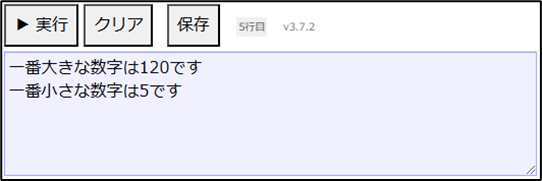
「切り上げ」や「切り捨て」という関数は引数として小数を()の中に入れるとそれぞれ小数を切り上げや切り捨てた整数の値を戻します。
「切り上げ」や「切り捨て」関数の引数は必ず1つだけです。
!DNCL2
x = 4.6
y = 切り上げ(x)
z = 切り捨て(x)
表示する(x , "の切り上げは" , y , "切り捨ては" , z , "です")上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます。
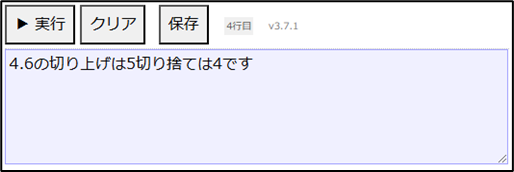
「乱数」という関数は引数として2つの値を()の中に入れると、2つの数字の間のどれかの値をランダムで戻します この関数の引数は必ず2つで左の引数(第一引数)が右の引数(第二引数)
よりも小さい値となる必要があります。
!DNCL2
表示する("毎回1~10のどれかを表示します。")
x = 乱数(1,10)
表示する(x)上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます。
※結果の数字は1~10の範囲で毎回ランダムに変わります。
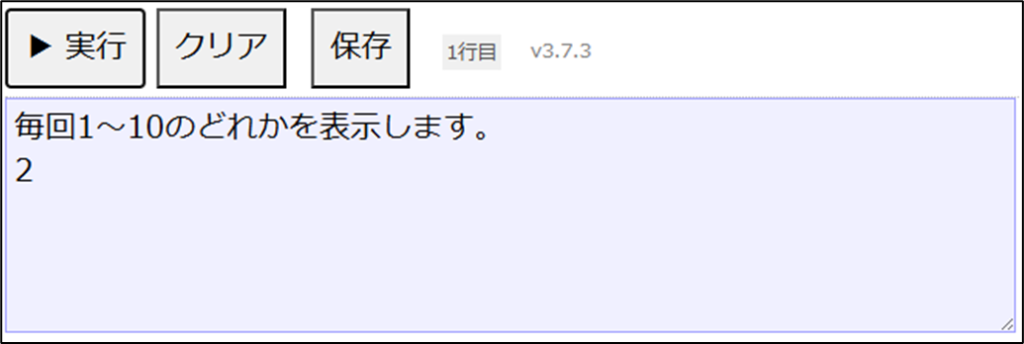
「二乗」という関数は引数として1つの値を()の中に入れると、二乗した結果を戻します。
!DNCL2
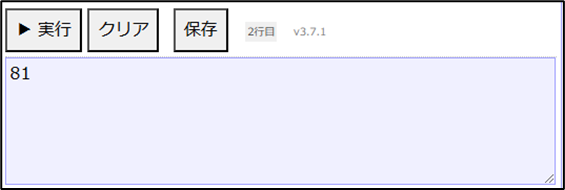
x = 二乗(5)
表示する(x)上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます。
「べき乗」という関数は引数として2つの値を()の中に入れると、左の引数(第一引数)を右の引数(第二引数)乗した結果を戻します。
!DNCL2
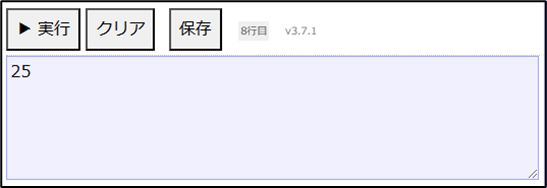
x = べき乗(3,4)
表示する(x)上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます。
このように組み込み関数は色々な種類が用意されています。
12 ユーザー定義関数
関数は元から用意されている「組み込み関数」以外に、自分で新しく定義して作ることも出来ます。
このような自分で定義する関数のことを「ユーザー定義関数」と言い、プログラムの中で何度も同じ処理をしたい時に呼び出して使用するとプログラムの行数を減らすことが出来て効率的です。
関数を自分で新しく定義する際は以下のように書きます。
関数 関数名(引数名)を
処理内容
と定義する
例えば引数で指定した値xを半径として円の面積を表示する「円面積」という関数を作ってみます。
!DNCL2
関数 円面積(x)を
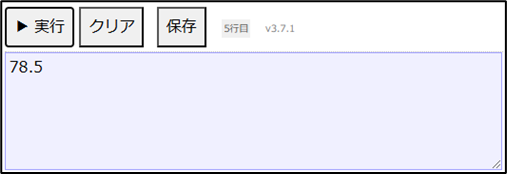
表示する(x * x * 3.14)
と定義する
円面積(5)上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます
関数の中から別の関数を呼び出すことも出来ます。
先ほどの「円面積」の中で引数を二回掛けている部分を「二乗」関数に置き換えてみましょう。
!DNCL2
関数 円面積(x)を
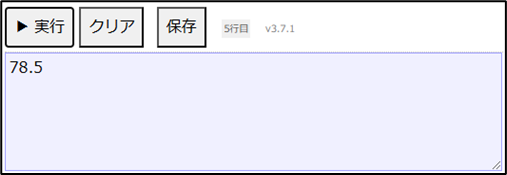
表示する(二乗(x) * 3.14)
と定義する
円面積(5)上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます。
今度は「組み込み関数」のように、関数で処理した結果を受け取ってみましょう
ちなみに処理した結果のことを「戻り値(もどりち)」と言います。
!DNCL2
関数 円面積(x)を
x * x * 3.14を戻す
と定義する
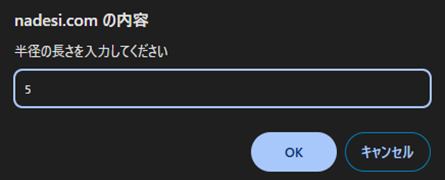
"半径の長さ(cm)を入力してください"と尋ねてhankeiに代入
menseki = 円面積(hankei)
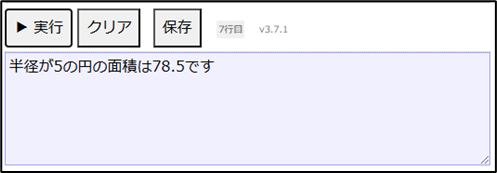
表示する("半径が", hankei , "cmの円の面積は", menseki , "㎠です")上記のように記述し、「▶実行」ボタンをクリックすると以下のような入力フォームが表示されるので値を入力して「OK」をクリックすると結果が表示されます。
ここまでの内容をちゃんと理解できているか確認するため、最後に演習問題5に取り組んでもらいます。
すぐに解答を見ないで自分でよく考えて実際にプログラムを書いてみてください。
演習問題5
これまで学習した知識を使って以下のプログラムを作ってみましょう。
ルール1) 「体積」という関数を定義し縦横高さを表す3つの引数(x , y , z)を掛けた結果を戻す
ルール2)以下の4つの茶色い立体の体積をルール1の「体積」関数を用いてそれぞれ求めて、それらを全て足し合わせた合計の体積を表示する(それぞれの立体の縦横高さは以下の通り)
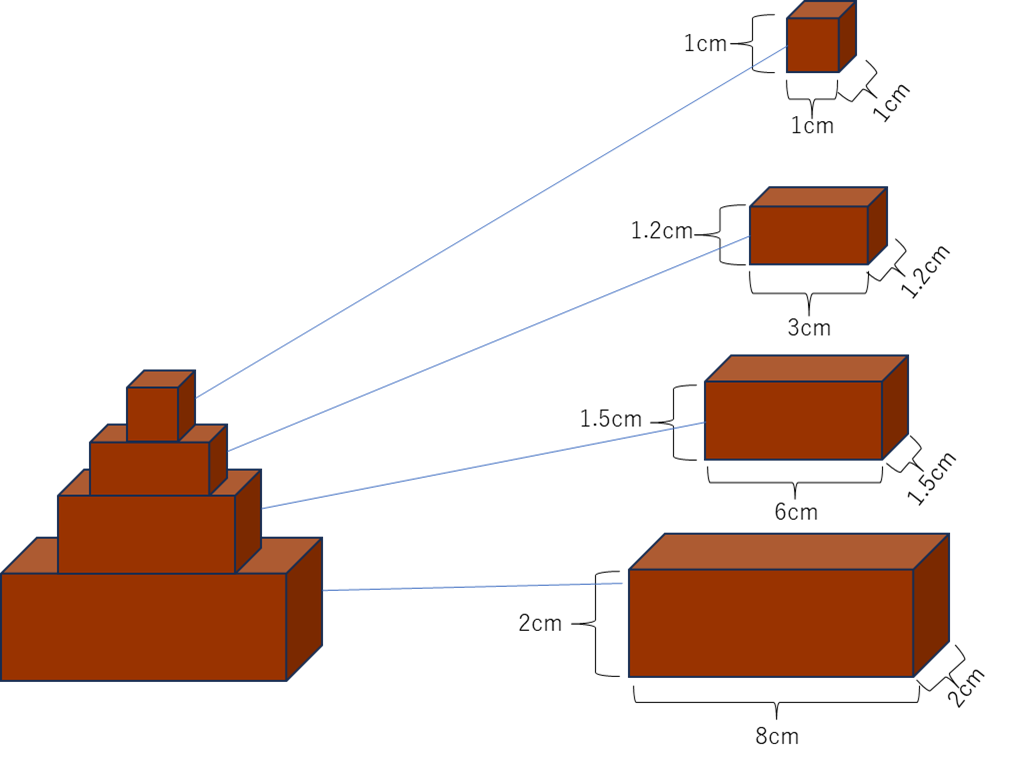
以下はプログラムを実行したときのイメージ

演習問題5解答
!DNCL2
関数 体積(x , y , z)を
x * y * z を戻す
と定義する
goukei = 体積(1,1,1) + 体積(1.2,3,1.2)+体積(1.5,6,1.5)+体積(2,8,2)
表示する("体積は", goukei ,"㎤です")以上でDNCLの学習は一通り終了です、お疲れさまでした。
プログラミング言語の中でもDNCLは日本語というかなり個性的な言語で、疑似プログラミング言語と呼ばれるように実際のシステム開発やアプリ開発で使用されることはありません。あくまで共通テストのプログラミング対策としてはDNCLの学習だけでも大丈夫ですが、プログラミングの学習はもっと奥が深くて楽しい要素がいっぱいありますので、ぜひDNCL以外にも興味を持って色々なプログラミング言語を学んでみることをお勧めします。



コメント