DNCL（実践５） - Guide and Geek

前回の記事でDNCLの「演習問題2」～「9 配列」までご説明しました
今回も「なでしこ」というサイトの「なでしこ３簡易エディタ」を使ってプログラムを書いていきます
必ず1行目に半角で「!DNCL2」もしくは全角で「！DNCL２」と記述してください

引用元：なでしこ３簡易エディタ
著作権：kujirahand

演習問題3
10 二次元配列

演習問題3

これまで学習した知識を使って以下のプログラムを作ってみましょう

ルール1) Cardという配列を作って、順番に8つの数字 10 , 50 , 20 , 100 , 30 , 90 , 1000 , 1 を登録する
ルール2）goukeiという変数を作って、配列Cardの値をループで順番にgoukeiに足して、ループの後で合計を表示する
ルール3）ルール2で求めたgoukeiを配列Cardの値の数（要素数（Card））で割って平均を表示する

以下はプログラムを実行したときのイメージ

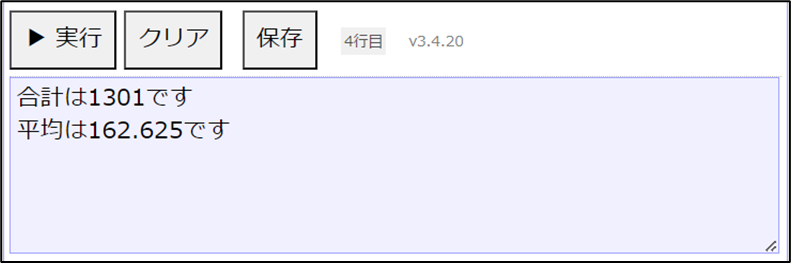
演習問題3解答

!DNCL2
Card = [10,50,20,100,30,90,1000,1]
goukei = 0
iを0から(要素数(Card) - 1)まで1ずつ増やしながら繰り返す:
　goukei = goukei + Card[i]
表示する("合計は", goukei , "です")
表示する("平均は", goukei / 要素数(Card) , "です")

10 二次元配列

配列は複数の値をまとめて保存するデータの列のことでした
例えば、テストの3科目（英語、国語、数学）の点数を左から順番に記録する配列Testは
Test = [80,65,77]のように[ ]の中に3つの数字をカンマで区切って並べました
二次元配列とは、この配列をいくつも縦に繋げたデータの表のことを言います
テストを例にA君、B君、C君、D君の4名が3科目のテストを受けた以下の結果の表を見てみましょう

	要素番号	0	1	2
要素番号	Test	英語	国語	数学
0	A君	80	65	77
1	B君	45	32	61
2	C君	20	14	8
3	D君	100	98	95

上記の表を二次元配列にするとTest = [[80,65,77],[45,32,61],[20,14,8],[100,98,95]]となります
つまり配列の中に4人それぞれの配列を入れ、配列と配列をカンマで区切っているイメージで
Test = [ A君配列 , B君配列 , C君配列 , D君配列 ]という構造になっています
二次元配列内のそれぞれの要素は配列名[縦の要素番号][横の要素番号]で指定します
分かりにくいので具体的にそれぞれの要素を以下に記載します

A君の英語80はTest[0][0]、国語65はTest[0][1]、数学77はTest[0][2]
B君の英語45はTest[1][0]、国語32はTest[1][1]、数学61はTest[1][2]
C君の英語20はTest[2][0]、国語14はTest[2][1]、数学8はTest[2][2]
D君の英語100はTest[3][0]、国語98はTest[3][1]、数学95はTest[3][2]

また、配列の時と同様に二次元配列の縦の要素番号と横の要素番号は変数名を使うことも出来ます

!DNCL2
Test=[ [80,65,77] , [45,32,61] , [20,14,8] , [100,98,95]]
iを0から3まで1ずつ増やしながら繰り返す：
　goukei = 0
　jを0から2まで1ずつ増やしながら繰り返す：
　　goukei = goukei + Test[i][j]
　表示する（i + 1 , "番目の生徒の合計は" , goukei , "点です"）

上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます

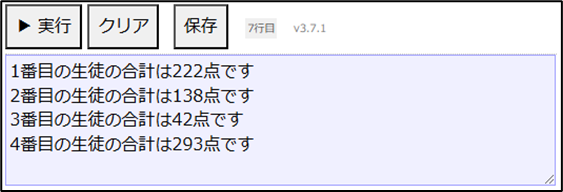
二次元配列の縦の要素の個数は要素数（配列名）で表します
二次元配列の横の要素の個数は要素数（配列名[縦の要素番号]）で表します

!DNCL2
Test=[ [80,65,77] , [45,32,61] , [20,14,8] , [100,98,95]]
表示する（"生徒の人数は" , 要素数（Test）,"人です"）
表示する（"1人目の受講科目数は" , 要素数（Test[0]）,"科目です"）
表示する（"2人目の受講科目数は" , 要素数（Test[1]）,"科目です"）
表示する（"3人目の受講科目数は" , 要素数（Test[2]）,"科目です"）

上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます

縦の要素の個数に比べて横の要素の個数は書き方が長いですね
その理由は、二次元配列は各行の横の要素の数が同じじゃない場合もあるからです
つまり二次元配列はデータの表が四角形の形ではなくても良いのです
例えば大学受験の共通テストは文系・理系や志望校が違うため生徒によって受ける科目数が違います
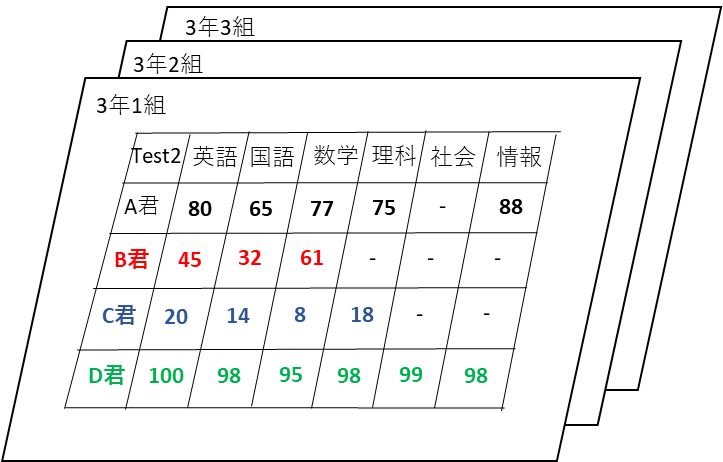
もう一度A君、B君、C君、D君が受けたテストの以下の結果の表を見てみましょう（「-」は未受験）

	要素番号	0	1	2	3	4	5
要素番号	Test2	英語	国語	数学	理科	社会	情報
0	A君	80	65	77	75	–	88
1	B君	45	32	61	–	–	–
2	C君	20	14	8	18	–	–
3	D君	100	98	95	98	99	98

各生徒の受講科目数と合計点と平均点を求めるプログラムを考えてみます
平均点を出すためには合計点を科目数で割る必要があるため、未受講の科目「-」を含めない二次元配列を考える必要があります

二次元配列 Test2 = [[80,65,77,75,88],[45,32,61],[20,14,8,18],[100,98,95,98,99,98]]となり
Test2 = [ A君配列 , B君配列 , C君配列 , D君配列 ]という構造になっています
プログラムを書く上での注意としてループ回数に気を付ける必要があります
二次元配列の縦の要素数は要素数（Test2）ですが要素番号は0から始まるので縦の要素のループは
変数iとするとiを0から（要素数（Test2）-1）まで1ずつ増やしながら繰り返す：となります
さらに、二次元配列の横の要素数は要素数（Test2[i]）ですが要素番号は0から始まるので横の要素のループは変数jとするとjを0から（要素数（Test2[i]）-1）まで1ずつ増やしながら繰り返す：となります

!DNCL2
Test2 = [[80,65,77,75,88],[45,32,61],[20,14,8,18],[100,98,95,98,99,98]]
表示する（"生徒の人数は" , 要素数（Test2）,"人です"）
iを0から(要素数（Test2）-1)まで1ずつ増やしながら繰り返す：
　goukei = 0
　jを0から(要素数（Test2[i])- 1)まで1ずつ増やしながら繰り返す：
　　goukei = goukei + Test2[i][j]
　表示する（i + 1 , "番目の生徒の受講科目数は", 要素数（Test2[i] ), "で合計は" , goukei , "点で平均は" , goukei / 要素数（Test2[i]） , "点です"）

上記のように記述し、「▶実行」ボタンをクリックすると以下の結果が表示されます

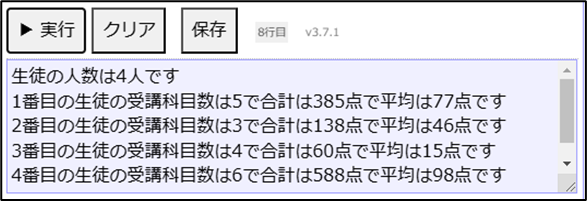
このような四角形ではないデータの表の形をした二次元配列のことを「ジャグ配列」といいます

今回は二次元配列について学習しましたがかなりややこしかったと思います
しかし二次元配列をさらに複雑にした三次元配列というのもあります
例えば上記の二次元配列が1クラス分のテストの成績を表していて、全部で3クラスあった場合などは、上記の二次元配列をさらに3個セットにした三次元配列を考える必要があります